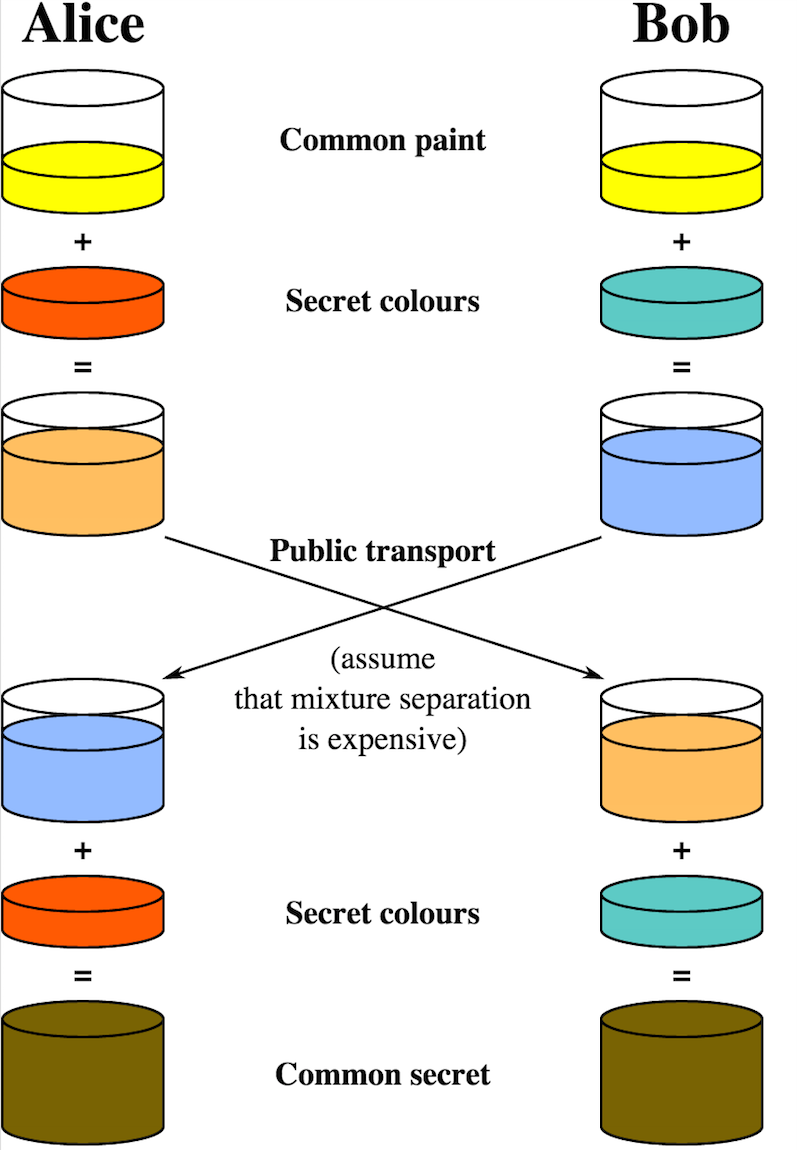
理解 Deffie-Hellman 密钥交换算法
再拾此书时,怀念 4 年前阳光明媚的午后,我在浙大紫金港图书馆的三楼,梦回了中学奥数的小伙伴,和那时曾想证明哥德巴尔猜想的情怀!
Deffie-Hellman 算法简介
Deffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一,它使得通信的双方能在非安全的信道中安全的交换密钥,用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法,之后被应用于安全领域,比如 Https 协议的 TSL(Transport Layer Security) 和 IPsec 协议的 IKE(Internet Key Exchange) 均以 DH 算法作为密钥交换算法。
数论知识
理解 DH 算法前,先介绍一些必要的数论领域知识,分别是离散对数问题和一个求模公式。
离散对数问题
假定 a, p 均是素数,下面两个集合相等,证明过程请参考 Cryptography and Network Security 第八章:
{ a^1 mod p, a^2 mod p, ..., a^(p-1) mod p } = {1, 2, ... , p-1 } {} 表示集合
上述式子可概括成以下三点,对于 1 <= x,y <= p - 1,有:
- a^x mod p 一定属于 {1, 2, …, p -1 }
- 如果 x != y,则 a^x mod p != a^y mod p
- 对于 1 <= b <= p - 1,一定存在唯一的 1 <= x <= p-1,使得 b = a^x mod p
第三点在求解上有这么一个特点:已知 x 求 b 非常容易,已知 b 求 x 非常困难,特别当 p 很大时,求解的复杂度非常高,所以它又被称为离散对数问题 (Discrete logarithm),它是 DH 算法能够安全交换密钥的基础!
求模公式
假设 q 为素数,对于正整数 a,x,y,有:
(a^x mod p)^y mod p = a^(xy) mod p
证明如下:
令 a^x = mp + n, 其中 m, n 为自然数, 0 <= n < p,则有
C = (a^x mod p)^y mod p
= ((mp + n) mod p)^y mod p
= n^y mod p
= (mp +n)^y mod p
= a^(xy) mod p
Deffie-Hellman 算法原理
本文参考 Cryptography and Network Security 一书,介绍 DH 算法原理,在掌握上节数论知识的基础上,理解 DH 算法原理非常容易。
假设 A, B 两方进行通信前需要交换密钥,首先 A, B 共同选取 p 和 a 两个素数,其中 p 和 a 均公开。之后 A 选择一个自然数 Xa,计算出 Ya,Xa 保密,Ya 公开;同理,B 选择 Xb 并计算出 Yb,其中 Xb 保密,Yb 公开。之后 A 用 Yb 和 Xa 计算出密钥 K,而 B 用 Ya 和 Xb 计算密钥 K,流程如下:
+-------------------------------------------------------------------+
| Global Pulic Elements |
| |
| p prime number |
| a prime number, a < p |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
| User A Key Generation |
| |
| Select private Xa Xa < p |
| Calculate public Ya Ya = a^Xa mod p |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
| User B Key Generation |
| |
| Select private Xb Xb < p |
| Calculate public Yb Yb = a^Xb mod p |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
| Calculation of Secret Key by User A |
| |
| Secret Key K K = Yb^Xa mod p |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
| Calculation of Secret Key by User B |
| |
| Secret Key K K = Ya^Xb mod p |
+-------------------------------------------------------------------+
下面证明,A 和 B 计算出来的密钥 K 相同。
K = Yb^Xa mod p
= (a^Xb mod p)^Xa mod p
= a^(Xa * Xb) mod p 根据上述求模公式
= (a^Xa mod p)^Xb mod p
= Ya^Xb mod p
上面一共出现了 a, p, Xa, Ya, Xb, Yb, K 共 7 个数,其中:
- 公开的数:a, p, Ya, Yb
- 非公开数:Xa, Xb, K
通常情况下,a 一般为 2 或 5,而 p 的取值非常大,至少几百位,Xa 和 Xb 的取值也非常大,其复杂度至少为 O(p^0.5)。对于攻击者来说,已知 Ya,Xa 的求解非常困难,同理 Xb 的求解也很困难,所以攻击者难以求出 K,所以 DH 能够保证通信双方在透明的信道中安全的交换密钥。下图非常形象的描述密钥交换流程: