理解 RSA 算法
Public-key Cryptography 简介
Public-key cryptography (公开密钥加密) 又称 asymmetric cryptography (非对称加密),即存在两把不同的密钥,分别称为公钥 Pu 和私钥 Pr,公钥通常用来加密明文 M,只有私钥才能解密密文 C,如果用 E 和 D 分别表示加密和解密算法,那么有:
C = E(Pu, M)
M = D(Pr, C)
下图(摘自维基百科)形象的表述了加密和解密流程:
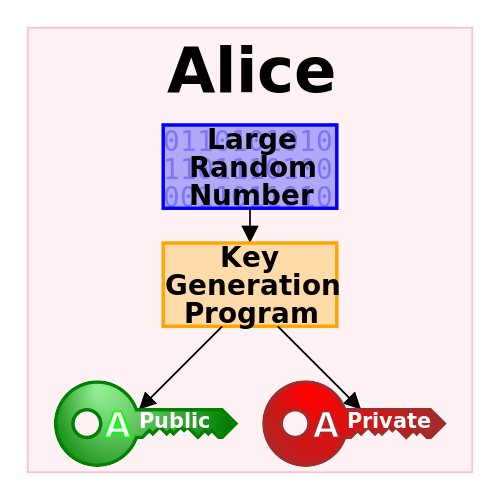
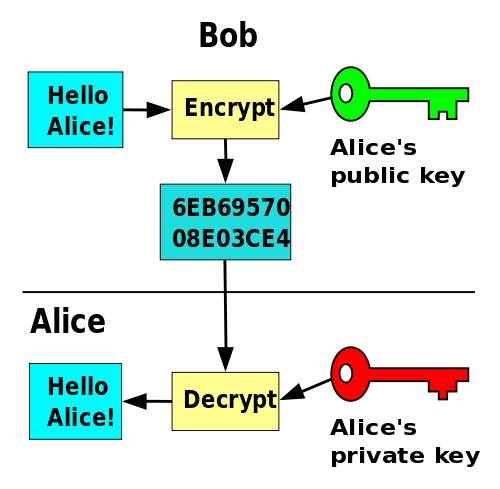
传统的对称加密需双方共享相同的密钥,通信安全很大程度依赖双方是否能妥善的管理密钥。公开密钥加密发明是密码学最为重要的里程碑之一,它从数学的角度保证了通信安全。公开密钥加密体系有三大范畴:
- Encryption/Decryption:即加密与解密,发送方用接收方的公钥加密消息
- Digital Signature:数字签名,发送方用私钥加密消息摘要生成签名,保证消息的完整性和可靠性
- Key Exchange:安全的交换密钥,通常用于交换对称加密的密钥
公钥加密有多种算法,最有名的的是 RSA 和 DH 等,如下:
+----------------+-----------------------+-------------------+--------------+
| Algorithm | Encryption/Decryption | Digital Signature | Key Exchange |
+----------------+-----------------------+-------------------+--------------+
| RSA | Yes | Yes | Yes |
+----------------+-----------------------+-------------------+--------------+
| Deffie-Hellman | No | No | Yes |
+----------------+-----------------------+-------------------+--------------+
| Elliptic Curve | Yes | Yes | Yes |
+----------------+-----------------------+-------------------+--------------+
| DSS | No | Yes | No |
+----------------+-----------------------+-------------------+--------------+
数论知识
理解 RSA 算法前,先介绍一些必要的数论领域知识。
欧拉函数
对正整数 n,欧拉函数 指小于 n 且与 n 互质的正整数数目,通常用 φ(n) 表示。
对于素数 p,有:
φ(p) = p - 1
对于素数 p, q 有:
φ(p * q) = φ(p) * φ(q) = (p - 1) * (q - 1)
如 φ(21) = 2 * 6 = 12
欧拉定理
对于正整数 a 和 n,欧拉定理有:
a^φ(n) mod n = 1
即:a^(φ(n) + 1) mod n = a mod n
模反元素
当 a, n 互质,一定存在模仿元素 b,使得:
a * b mod n = 1
由欧拉定理可知:
1 = a^φ(n) mod n = a * a^(φ(n) - 1) mod n
可求得一个 b = a^(φ(n) - 1),满足 a * b mod n = 1
RSA 算法原理
RSA 简介
RSA 算法于 1977 由 Ron Rivest,Adi Shamir 和 Leonard Adleman 提出,是目前应用最为广泛的非对称加密算法。极大数分解难题是 RSA 算法可靠性的根基,即给定两个大素数 p 和 q,其中 n = p * q,有:
已知 p、q,求 n = p * q 很容易
已知 n,求 p、q,并且 p * q = n 很困难
RSA 原理
对于明文 M 和 密文 C,且 M < n, C < n,其加密和解密过程如下:
C = M^e mod n
M = C^d mod n
上述公式可表述为:
M = M^(e * d) mod n
根据欧拉定理可知:
只需 e * d mod φ(n) = 1,即可满足上式
如果我们选取素数 p, q,那么:
n = p * q 容易计算
φ(n) = (p - 1) * (q - 1) 容易计算
很容易选取一个正整数 e,e 和 φ(n) 互质
当 e 和 φ(n) 互质时:
由欧拉定理可很容易算出一个模反元素 d,满足 e * d mod φ(n) = 1
RSA 流程
Cryptography and Network Security 形象的描述了 RSA 流程:
+-------------------------------------------------------------------------------+
| Key Generation |
| |
| Select p, q p and q both prime, p != q |
| Calculate n = p * q |
| Calculate φ(n) = (p - 1) * (q - 1) |
| Select integer e e is relatively primte to φ(n) |
| Calculate d (d * e) mod n = 1 |
| Public key PU = {e, n} |
| Private key PR = {d, n} |
+-------------------------------------------------------------------------------+
+-------------------------------------------------------------------------------+
| Encryption |
| |
| Plaintext M M < n |
| Ciphertext C C = M^e mod n |
+-------------------------------------------------------------------------------+
+-------------------------------------------------------------------------------+
| Decryption |
| |
| Ciphertext C C |
| Plaintext M M = C^d mod n |
+-------------------------------------------------------------------------------+