下列两个循环哪个快？

int array[1024][1024]

// Loop 1
for(int i = 0; i < 1024; i ++)
    for(int j = 0; j < 1024; j ++)
        array[i][j] ++;

// Loop 2
for(int i = 0; i < 1024; i ++)
    for(int j = 0; j < 1024; j ++)
        array[j][i] ++;

Loop 1 的 CPU cache 命中率高，所以它比 Loop 2 约快八倍！

Gallery of Processor Cache Effects 用 7 个源码示例生动的介绍 cache 原理，深入浅出！但是可能因操作系统的差异、编译器是否优化，以及近些年 cache 性能的提升，第 3 个样例在 Mac 的效果与原文相差较大。另外 Berkeley 公开课 CS162 图文并茂，非常推荐。本文充当搬运工的角色，集二者之精华科普 CPU cache 知识。

What is Cache

维基百科定义为：在计算机系统中，CPU cache（中文简称缓存）是用于减少处理器访问内存所需平均时间的部件。在金字塔式存储体系中它位于自顶向下的第二层，仅次于 CPU 寄存器。其容量远小于内存，但速度却可以接近处理器的频率。

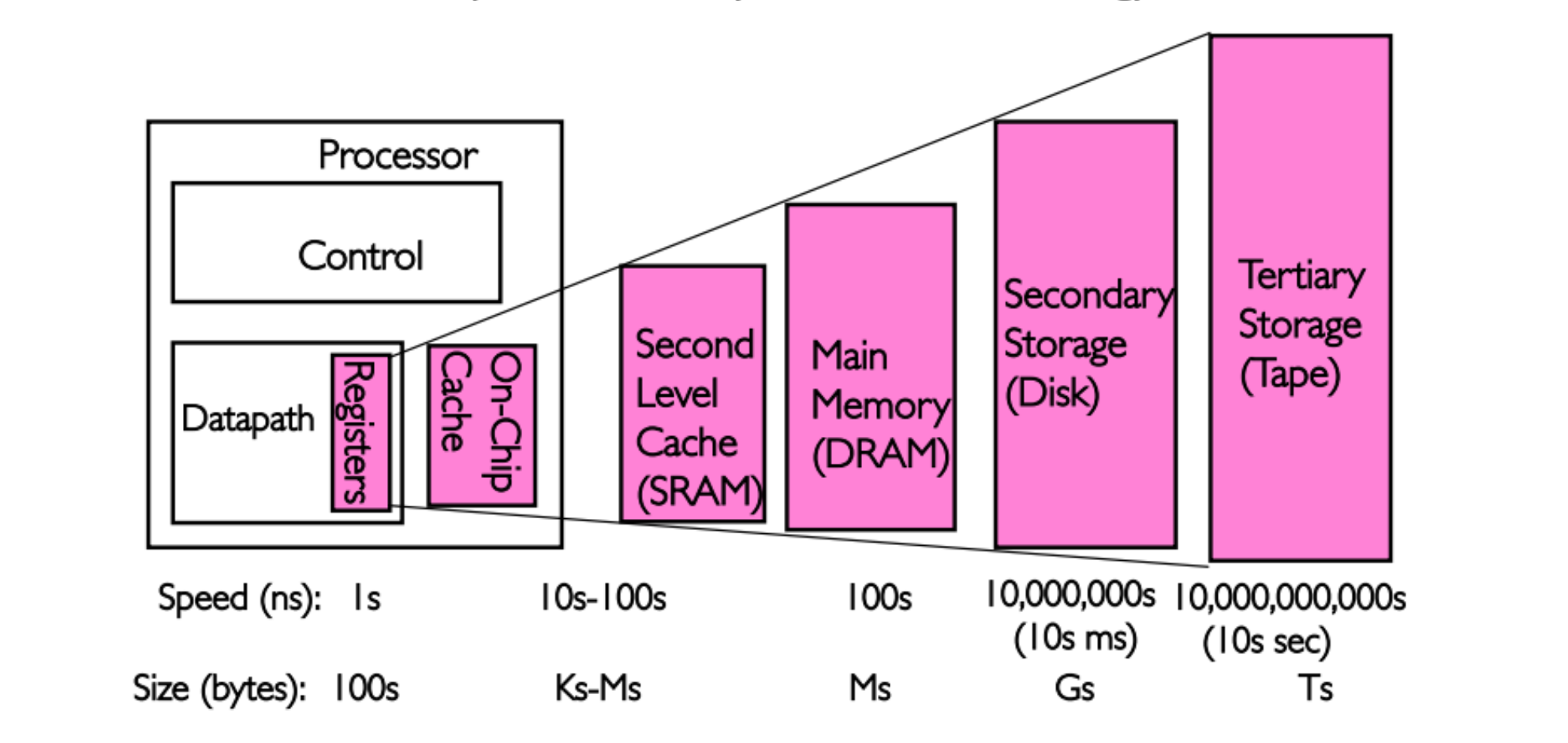
hierarchy

原图出处(CS162)。 Note: 早期的 L2 cache 位于主板，现在 L2 和 L3 cache 均封装于 CPU 芯片。

CPU 访问内存时，首先查询 cache 是否已缓存该数据。如果有，则返回数据，无需访问内存；如果不存在，则需把数据从内存中载入 cache，最后返回给理器。在处理器看来，缓存是一个透明部件，旨在提高处理器访问内存的速率，所以从逻辑的角度而言，编程时无需关注它，但是从性能的角度而言，理解其原理和机制有助于写出性能更好的程序。Cache 之所以有效，是因为程序对内存的访问存在一种概率上的局部特征：

  • Spatial Locality：对于刚被访问的数据，其相邻的数据在将来被访问的概率高。
  • Temporal Locality：对于刚被访问的数据，其本身在将来被访问的概率高。

从广义的角度而言，cache 可以分为两类：

  • 数据(指令) cache: 缓存内存数据，根据层级又可分为 L1、L2 和 L3，如果 miss，CPU 需访内存获取数据(指令)。
  • TLB(Translation lookaside buffer): 寻址 cache，缓存进程的虚拟机地址和物理地址之间的映射关系，如果 miss，MMU 需多次访问内存获取多级 page table 才能计算出物理地址。

比 mac OS 为例，可用 sysctl 查询 cache 信息。

$ sysctl -a

hw.cachelinesize: 64
hw.l1icachesize: 32768
hw.l1dcachesize: 32768
hw.l2cachesize: 262144
hw.l3cachesize: 3145728
machdep.cpu.cache.L2_associativity: 8
machdep.cpu.core_count: 2
machdep.cpu.thread_count: 4
machdep.cpu.tlb.inst.large: 8
machdep.cpu.tlb.data.small: 64
machdep.cpu.tlb.data.small_level1: 64
machdep.cpu.tlb.shared: 1024

如下图：

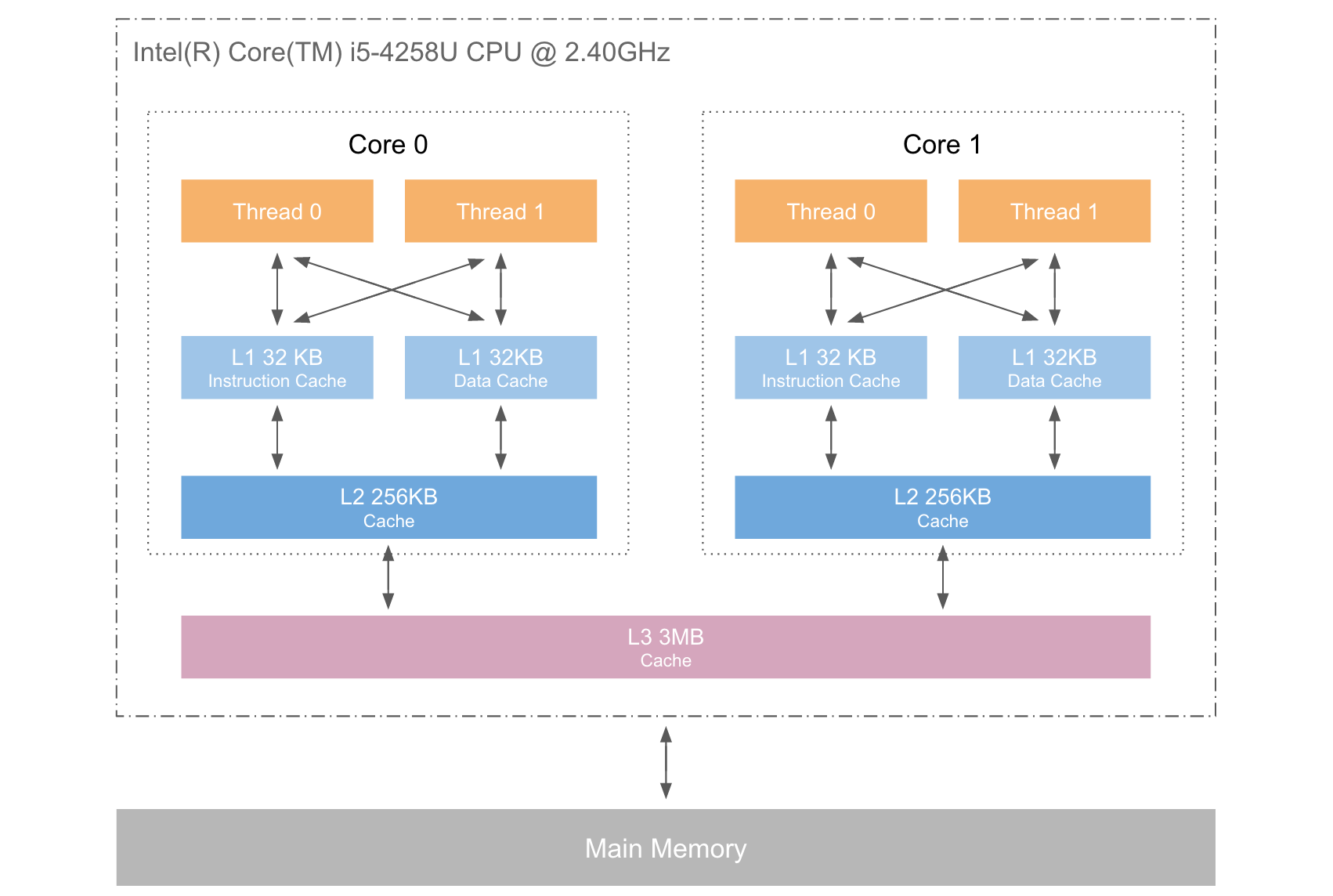
cpu cache

Why Cache

早期的 CPU 并没有 cache，以起于 1978 年的 intel x86 芯片为例，它从 1992 年开始才开始引入 cache：

  • 1992: 386 platform 引入 L1 cache
  • 1995: Pentium Pro 引入 L2 cache
  • 2008: Core i3 引入 L3 cache

CPU 和 RAM 主频的增长速率的巨大差距是 cache 引入的直接原因，下图展示了从 1980 年到 2010 年二者的发展状况，CPU 性能的年增长速度约为 60%，而 RAM 仅有约 9%，巨大的差异导致数十年后，CPU 的速度约比 RAM 快数百倍。

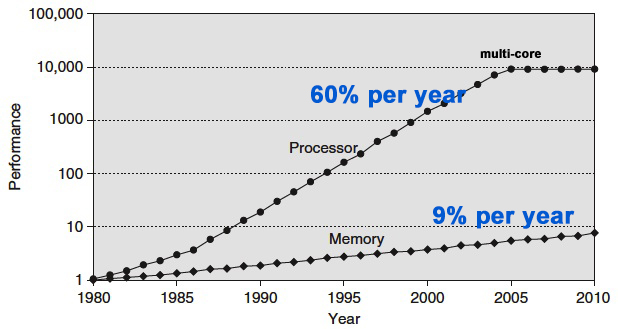
history

原图出处: Computer Architecture, A quantitative Approach by Hennessy and Patterson

有人问，为什么不提高 RAM 的速度，因为成本太高！成本因素也是 cache 分为多级的原因。越快的越贵，所以容量小；越慢越廉，容量可很大，它是成本和性能之间的折中方案。CS162 如下两句原话很好的概括了 cache 的作用。

  • Present as much memory as in the cheapest technology
  • Provide access at speed offered by the fastest technology

Understand Cache With Some Cases

本节采用 Gallery of Processor Cache Effects 的例子，加以图文，介绍 cache 的机制，其中除了 L1, L2 and L3 cache size 小节的样例外，其它样例在本人的 mac 中均得到很好的复现。

Cache line size

Cache line 是 cache 和 RAM 交换数据的最小单位，通常为 64 Byte。当 CPU 把内存的数据载入 cache 时，会把临近的共 64 Byte 的数据也一同载入，因为临近的数据在将来被访问的可能性大，这为 spatial locality 奠定了基础。本文开头的例子中，因为 loop 1 依次访问的数据在地址空间上是相邻的，故 cache 命中率高，耗时少。下列展示了如何测试 cache line 的 size:

double diff, total_time = 0;
struct timeval t1, t2;
char *array, *clear_array;

array = malloc(ARRAY_SIZE * sizeof(char));
clear_array = malloc(L3_SIZE * sizeof(char));

for(int t = 0; t < TIMES; t++)   //loop for many times
{
    gettimeofday(&t1, NULL);
    for(int i = 0; i < ARRAY_SIZE; i += stride){
        array[i]++;
    }
    gettimeofday(&t2, NULL);
    diff = time_diff(t1, t2);
    total_time += diff;

    //clear array data in L1,L2,L3 cache
    for(int i = 0; i < L3_SIZE; i ++){
        clear_array[i] ++;
    }
}

经归一化处理后，本人所测 array[i] ++ 的平均时间与 stride 的关系如下(如果关闭 hardware prefetch，效果可能会更好)：

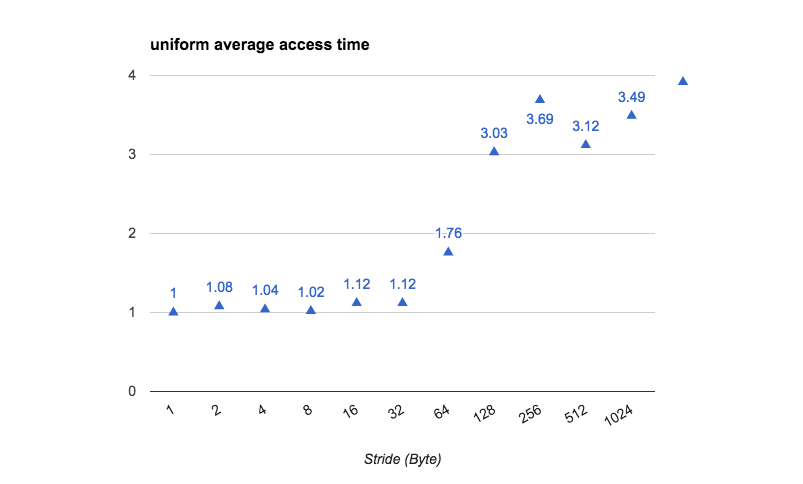
cpu cache line size

L1、L2 and L3 cache size

L1, L2 和 L3 cache size 的测试方法如下，在循环内每隔 64 Byte(cache line) 访问 array 一次：

int steps = 64 * 1024 * 1024; // Arbitrary number of steps
int length_mod = ARRAY_SIZE - 1;

for (int i = 0; i < steps; i += 64)
{
    array[i & length_mod]++; // (x & length_mod) is equal to (i % length)
}

所得结果为：

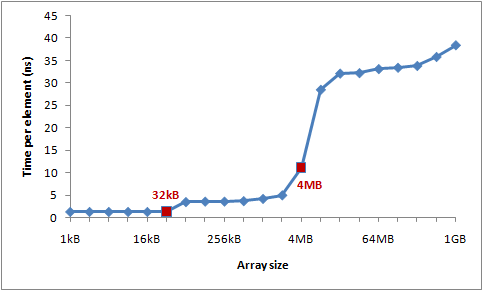
cpu l cache

原图出处 Gallery of Processor Cache Effects 注：本例在本人 Mac 的效果远远差于原著的效果，故采用原图。

对于当前个人计算机的 CPU，L1 cache 通常为数十 KB，L2 cache 为数百 KB，L3 cache 可达数 MB，但是 TLB 相对较小，一般只有几百个 entry。

Instruction-level parallelism

下列循环哪个快？

# Loop 1
gettimeofday(&t1, NULL);
for(int i = 0; i < ARRAY_SIZE - 1; i++){
    array[0] ++;
    array[0] ++;
}

# Loop 2
gettimeofday(&t2, NULL);
for(int i = 0; i < ARRAY_SIZE - 1; i++){
    array[0] ++;
    array[1] ++;
}

gettimeofday(&t3, NULL);

loop1_time = time_diff(t1, t2);
loop2_time = time_diff(t2, t3);

Loop 2 的速度比 Loop 1 接近快一倍。

目前 CPU 可以实现一定程度上的并行，比如在同一个时间点访问 L1 Cache 上的两处数据，也可以在同一个时间点执行两条算术运算指令。对于 Loop 2，它并行的运行 array[0] ++ 和 array[1] ++。

Loop 1

cpu cache loop1

原图出处 Gallery of Processor Cache Effects

Loop 2

cpu cache loop1

原图出处 Gallery of Processor Cache Effects

Cache associativity

本节主要介绍内存中的数据在 cache 的存放规则，即对于给定地址的数据 A，它该存放在 cache 的何处？要回答此问题，首先需介绍三种不同的存放规则：

  • Direct mapped cache: 数据 A 在 cache 的存放位置只有固定一处。
  • N-way set associative cache: 数据 A 在 cache 的存放位置可以有 N 处。
  • Full associative cache: 数据 A 可存放在 cache 的任意位置。

从硬件的角度出发，direct mapped cache 设计简单，full associative cache 设计复杂，特别当 cache size 很大时，硬件成本非常之高。但是在 direct mapped cache 下数据的存放地址是固定唯一的，所以容易产生碰撞，最终降低 cache 的命中率，影响性能。在成本和性能的权衡下，当前的 CPU 都是 N-way set associative cache，N 通常为 4，8 或 16。

以大小为 32 KB，cache line 的大小为 64 Byte 的某 cache 为例，对于不同存放规则，其硬件设计也不同，下列图片依次展示其原理。

Direct mapped cache

direct mapping

2-way set associative

two way associative

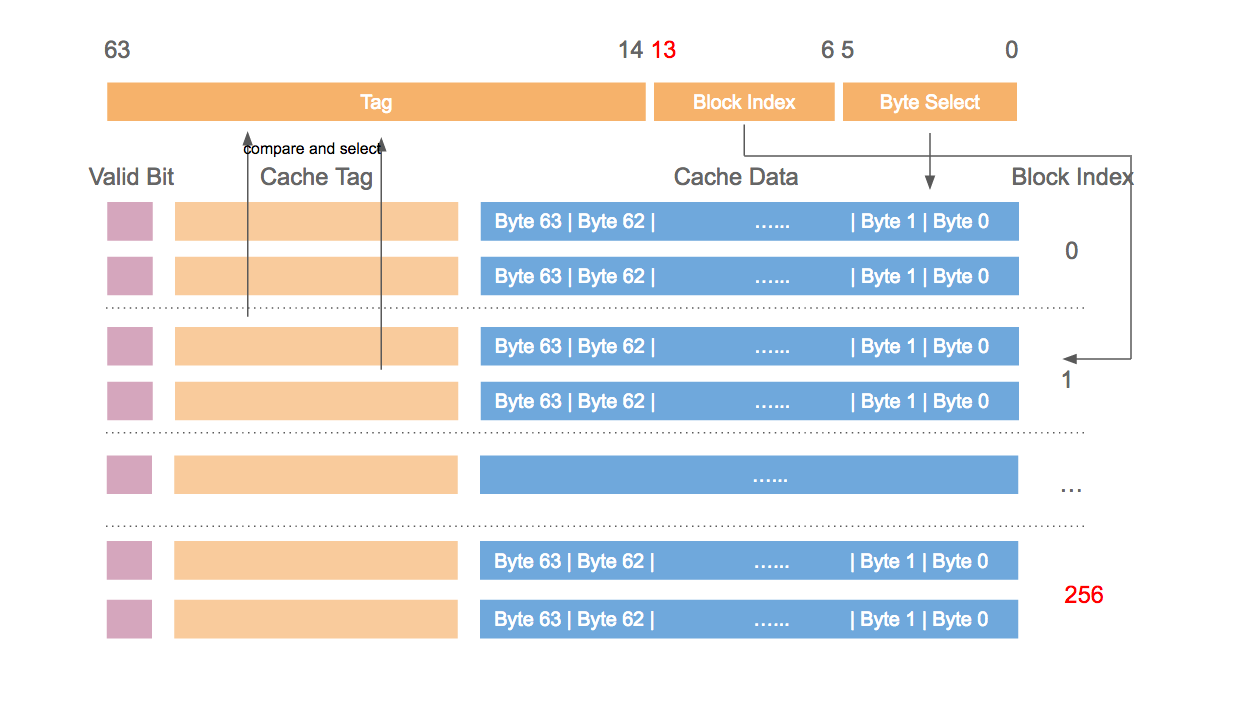
Full associative cache

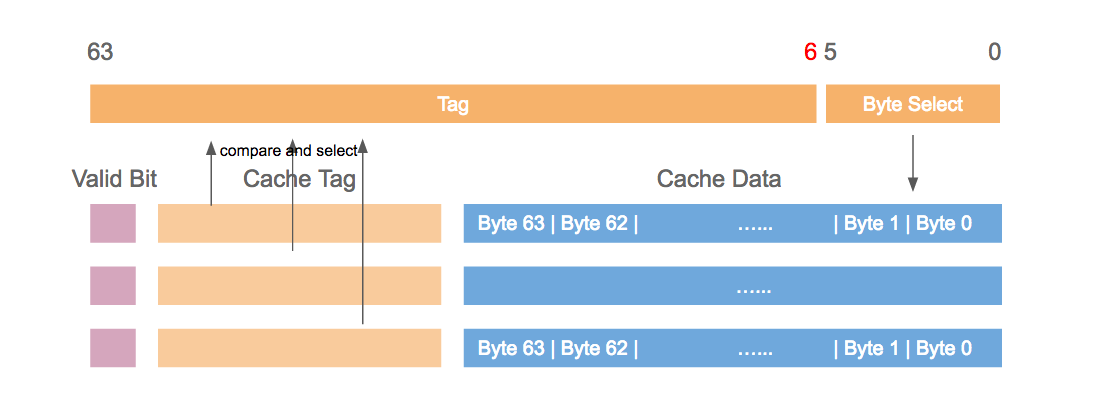
full associative

本人的 L2 cache 大小为 256 KB，8-way set associative，cache line 为 64 Byte，所以共有 512 个 set (256 K / 64 / 8)，所以地址间隔 32768 (512 * 64) 个 Byte 的数据都会落在 cache 的同一个 set 中。

#define ARRAY_SIZE  64 * 1024 * 1024
#define STEPS       1024 * 1024 * 1024

for(int i = 0; i < STEPS; i++){
    array[p] ++;
    p += STRIDE;
    if(p >= ARRAY_SIZE)
        p = 0;
}

当 STRIDE 为 32768 时，array[p] 总是访问相同 cache set，造成大量的冲突和置换，所用时间为 18 s，当 STRIDE 为 1 时，所用时间为 3.5 s。

False cache line sharing

以本计算机的 CPU(Intel(R) Core(TM) i5-4258U CPU @ 2.40GHz) 为例，同一个 core 里的两个 cpu thread 共享 L1 和 L2 cache，L3 cache 则是由 2 个 core 共享。但一个 cpu thread 修改 cache 的某处时，该处所在的整个 cache line 都会被置为 invalid，其它的 cpu thread 不能使用该 cache line，直到数据被同步到 RAM 中。

int counter[1024]; // global variable

void *update_counter(int position)
{
    for(int i = 0; i < 1000000000; i ++ ){
        counter[position] ++;
    }
}

int main()
{
    double diff;
    struct timeval t1, t2;
    pthread_t tid1, tid2, tid3, tid4;

    // Sharing
    gettimeofday(&t1, NULL);
    pthread_create(&tid1, NULL, update_counter, (void *)1);
    pthread_create(&tid2, NULL, update_counter, (void *)2);
    pthread_create(&tid3, NULL, update_counter, (void *)3);
    pthread_create(&tid4, NULL, update_counter, (void *)4);

    pthread_join(tid1, NULL);
    pthread_join(tid2, NULL);
    pthread_join(tid3, NULL);
    pthread_join(tid4, NULL);
    gettimeofday(&t2, NULL);
    diff = time_diff(t1, t2);
    printf("%f\n", diff);

    // False Sharing
    gettimeofday(&t1, NULL);
    pthread_create(&tid1, NULL, update_counter, (void *)16);
    pthread_create(&tid2, NULL, update_counter, (void *)32);
    pthread_create(&tid3, NULL, update_counter, (void *)48);
    pthread_create(&tid4, NULL, update_counter, (void *)64);

    pthread_join(tid1, NULL);
    pthread_join(tid2, NULL);
    pthread_join(tid3, NULL);
    pthread_join(tid4, NULL);

    gettimeofday(&t2, NULL);
    diff = time_diff(t1, t2);
    printf("%f\n", diff);
}

并行创建 4 个线程执行上述函数，当 position 值分别为 1，2，3，4 时，所用总时间为 13.1 s，当值为 16，32，48，64 时，所用总时间为 3.4 s。

Hardware complexities

上述例子为我们介绍了 Cache 的基本原理，但是 CPU 还是非常复杂多样。例如：

int A, B, C, D, E, F, G;

for (int i = 0; i < 200000000; i++)
{
    <something> // do something
}

结果为：

<something>	           Time

A++; B++; C++; D++;	   719 ms
A++; C++; E++; G++;	   448 ms
A++; C++;	           518 ms

One more question

下列循环哪个快？

int array_512[512][512]
int array_513[513][513]

// Loop 1
for(int i = 0; i <  512; i++){
    for(int j = 0; j < 512; j ++){
        tmp = array_512[i][j];
        array_512[i][j] = array_512[j][i];
        array_512[j][i] = tmp;
    }
}

// Loop 2
for(int i = 0; i <  513; i++){
    for(int j = 0; j < 513; j ++){
        tmp = array_513[i][j];
        array_513[i][j] = array_513[j][i];
        array_513[j][i] = tmp;
    }
}