Python 求解数独
芬兰一位数学家号称设计出全球”最难”的”数独游戏”,并刊登在报纸上,让大家去挑战。这位数学家说,他所设计的数独游戏难度等级是十一,是所有数独游戏中难度最高的等级。
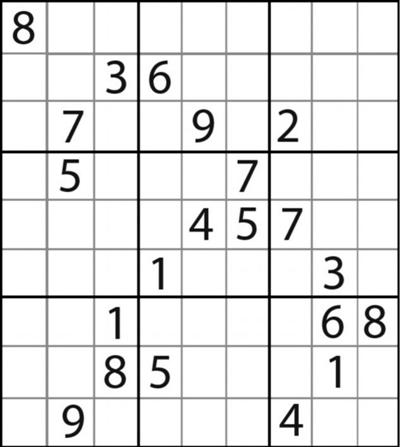
数独编程求解的方法有两种:
- 穷举法:穷举法算法简单,但运行时所花费的时间量大,这里主要讨论回溯法。
- 回溯法:按照深度搜索的方式进行。即在第一层选定一个满足约束条件的解,然后以该可能解为出发点,搜索第二层的一个可能解(试探)。如果搜索到第二层的一个可能解,则继续搜索第三层的一个可能解。依次类推,直到所有层的可能解都被找到,则得到了该问题的一个完整解。如果第二层所有的可能解都不满足约束条件,则返回第一层,放弃原有的可能解,使用第一层的下一个可能解(回溯)。以此类推,寻找第二层的一个可能解。
数独问题的约束条件为:
- 数值范围仅限于 1-9
- 行中不允许重复数字
- 列中不允许重复数字
- 小九宫内不允许重复数字
本文采用了简单的回溯算法求得如下结果,没在性能上做优化,关于算法性能,Peter Norvig 的文章 Solving Every Sudoku Puzzle 讲解的非常好。
8 1 2 | 7 5 3 | 6 4 9
9 4 3 | 6 8 2 | 1 7 5
6 7 5 | 4 9 1 | 2 8 3
------+-------+------
1 5 4 | 2 3 7 | 8 9 6
3 6 9 | 8 4 5 | 7 2 1
2 8 7 | 1 6 9 | 5 3 4
------+-------+------
5 2 1 | 9 7 4 | 3 6 8
4 3 8 | 5 2 6 | 9 1 7
7 9 6 | 3 1 8 | 4 5 2
代码如下:
class Suduko(object):
def __init__(self, s):
self.s = s
def check_all(self, i, j, value):
#检测s[i][j]=value时,是否满足数独约束
return self.check_row(i, j, value) and self.check_column(i, j, value)\
and self.check_small_sudoku(i, j, value)
def check_row(self, i, j, value):
#检测s[i][j]=value是否满足 行中不允许重复数字
return value not in self.s[i]
def check_column(self, i, j, value):
#检测s[i][j]=value是否满足 列中不允许重复数字
column = [self.s[v][j] for v in range(9)] return value not in column
def check_small_sudoku(self, i, j, value):
#检测s[i][j]=value是否满足 小九宫格不允许重复数字
small_sudoku = [self.s[m][n] for m in range(i/3*3,(i/3+1)*3)\ for n in range(j/3*3,(j/3+1)*3)]
return value not in small_sudoku
def recursion_search(self):
#回溯求解,如果i,j都大于等于8,表示求解OK
i,j = self.start_point()
if i >=8 and j >=8 and self.s[8][8]:
return True
for value in range(1,10):
if self.check_all(i, j, value):
self.s[i][j] = value #如果s[i][j]满足约束,则令s[i][j]=value
if not self.recursion_search():
self.s[i][j] = 0 #如果后面的递归搜索不满足要求,令s[i][j] = 0
else:
return True
return False #如果该点遍历1-9都不符合要求,则表示上游选值不当,回溯
def start_point(self):
for i in range(9):
for j in range(9):
if not self.s[i][j]:
return i,j
return i,j
if '__main__' == __name__:
s = [[8,0,0,0,0,0,0,0,0],
[0,0,3,6,0,0,0,0,0],
[0,7,0,0,9,0,2,0,0],
[0,5,0,0,0,7,0,0,0],
[0,0,0,0,4,5,7,0,0],
[0,0,0,1,0,0,0,3,0],
[0,0,1,0,0,0,0,6,8],
[0,0,8,5,0,0,0,1,0],
[0,9,0,0,0,0,4,0,0]]
S = Suduko(s)
S.recursion_search()
for i in range(9):
print S.s[i]